Skip to contents

Deeper Dive: Kolmogorov Distribution, Density, Random Variates

by Bruce J. Swihart

Source: vignettes/articles/deep_dive_kolm.Rmd
deep_dive_kolm.Rmd

Background

What does the Kolmogorov distribution have to do with multivariate product distributions? Turns out a distribution based on the Kolmogorov distribution – which is most commonly known for its development for and application in goodness-of-fit tests – is useful for making elliptically contoured multivariate logistic distributions.

There are two (equivalent) ways to represent the Kolmogorov distribution, in what is sometimes called a “limiting form” - which here means it involves an infinite sum. A third form is introduced, that “splices” the first two representations together:

Cumulative Distribution Function

Representation 1:

  • FK1(x)=1−2∑i=1∞(−1)i−1exp(−2i2x2)F_{K1}(x) = 1 - 2 \sum^{\infty}_{i=1} (-1)^{i-1} \exp{\left(-2 i^2 x^2\right)}

Representation 2:

  • FK2(x)=2πx∑i=1∞exp(−(2i−1)2π2/(8x2))F_{K2}(x) = \frac{\sqrt{2 \pi}}{x} \sum^{\infty}_{i=1} \exp{\left(-(2 i - 1)^2 \pi^2 / \left( 8 x^2\right) \right)}

Representation 3:

  • FK3(x)F_{K3}(x) is
    • FK2(x)∀x∈[0,xc)F_{K2}(x)~~\forall x \in [0,x_c)
    • FK1(x)∀x∈[xc,∞)F_{K1}(x)~~\forall x \in [x_c,\infty)

And taking the derivative with respect to xx, we get the corresponding limiting forms of the density:

Density

Representation 1:

  • fK1(x)=−2∑i=1∞(−1)i−1(−4i2x)exp(−2i2x2)f_{K1}(x) = - 2 \sum^{\infty}_{i=1} (-1)^{i-1} \left(-4 i^2 x\right) \exp{\left(-2 i^2 x^2\right)}

Representation 2:

  • fK2(x)=2π4x4∑i=1∞((2i−1)2π2−4x2)exp(−(2i−1)2π2/(8x2))f_{K2}(x) = \frac{\sqrt{2 \pi}}{4x^4} \sum^{\infty}_{i=1} \left((2 i - 1)^2 \pi^2 - 4x^2 \right) \exp{\left(-(2 i - 1)^2 \pi^2 / \left( 8 x^2\right) \right)}

Representation 3:

  • fK3(x)f_{K3}(x) is
    • fK2(x)∀x∈[0,xc)f_{K2}(x)~~\forall x \in [0,x_c)
    • fK1(x)∀x∈[xc,∞)f_{K1}(x)~~\forall x \in [x_c,\infty)
dkolm(1,rep="K1")
#> [1] 1.071949
dkolm(1,rep="K2")
#> [1] 1.071949
dkolm(1,rep="K3")
#> [1] 1.071949

Check expected value – should be π2ln2=\sqrt{\frac{\pi}{2}}\ln2 = 0.8687312…. One could do this with their own code, or they can use mpvd::dkolm:

  • own code / base R:
f <- function(x,nterms=1e5){ 
  k=1:nterms; 
  -2*sum( (-1)^(k-1) * -4*x*k^2 * exp(-2*k^2*x^2) )
}
f_vec <- Vectorize(f, "x")
x_f_vec <- function(x) x*f_vec(x,nterms=1e5)
integrate(x_f_vec,0,Inf)
#> 0.8687312 with absolute error < 1.7e-05
x_f_K1 <- function(x, nterms=1e5) x*dkolm(x,nterms,rep="K1")
x_f_K2 <- function(x, nterms=1e5) x*dkolm(x,nterms,rep="K2")
x_f_K3 <- function(x, nterms=1e5) x*dkolm(x,nterms,rep="K3")

mom1_K1 <- integrate(x_f_K1, 0, Inf)[1]
mom1_K2 <- integrate(x_f_K2, 0, Inf)[1]
mom1_K3 <- integrate(x_f_K3, 0, Inf)[1]

print(matrix(c(mom1_K1, mom1_K2, mom1_K3, sqrt(pi/2)*log(2)),ncol=1), digits=20)
#>      [,1]                  
#> [1,] 0.86873116063485644744
#> [2,] 0.86873116063489197458
#> [3,] 0.8687311606348562254 
#> [4,] 0.86873116063615907212

The printout shows agreement out to the 11th digit.

Next, we plot the densities and also print out some values.

The takeaways are:

  • K1K1 representation stuggles with small xx
  • K2K2 representation struggles with larger xx

Yet,

  • K2K2 representation is better with small xx
  • K1K1 representation is better with larger xx

And now we see the motivation for the construction of K3K3. Representation K3K3 uses K1K1 for larger xx values bigger than a cutpoint and K2K2 for xx values smaller than that cutpoint. The default value for the cutpoint is K3cutpt = 2. We pick nterms=10 to demonstrate the problems - in practice we pick the number of terms to be much higher, say 1e5, which makes the violations less egregious for moderate values of xx but the violations can still persist for extremely small and large values of xx. Therefore, solely increasing nterms may not be a solution (depending on the application) for K1K1 or K2K2. That’s why mvpd uses the ’’spliced” version K3K3 as well as a default of 100,000 terms.

Plot density

  • nterms=10
xdom <- c(seq(0.0,1,0.01), seq(1.1,6,.1), 8,10,12)
plot(xdom,dkolm(xdom,nterms=10,rep="K1"), main="K1 struggles with small x", ylab="", xlab="x")
abline(h=0,col="blue")
plot(xdom,dkolm(xdom,nterms=10,rep="K2"), main="K2 struggles with large x", ylab="", xlab="x")
abline(h=0,col="blue")

dkolm(12,rep="K2",nterms=10)
#> [1] -0.005592438
#> [1] -0.005592438 from rep="K2"

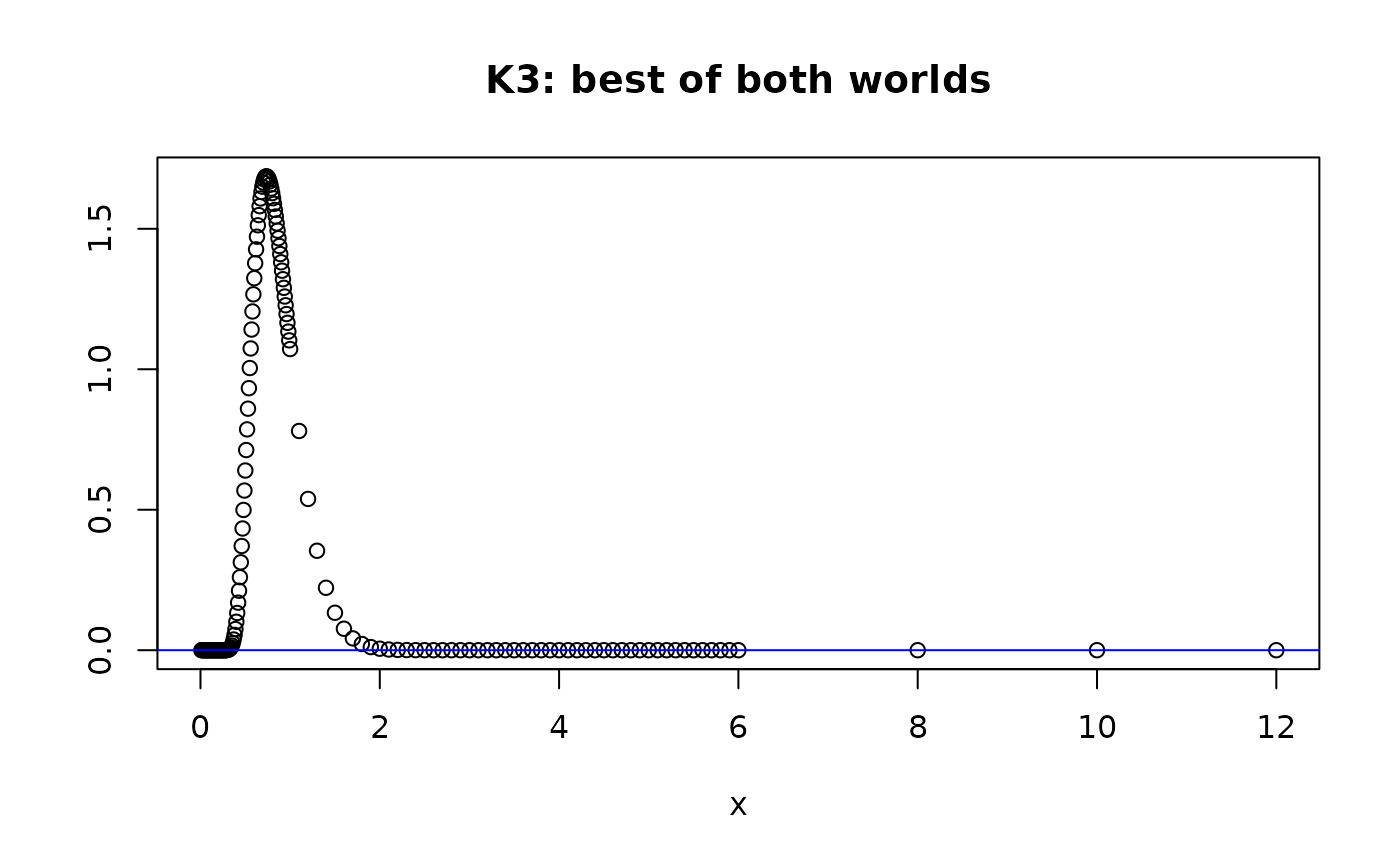
plot(xdom,dkolm(xdom,nterms=10,rep="K3"), main="K3: best of both worlds", ylab="", xlab="x")
abline(h=0,col="blue")
dkolm(12,rep="K3",nterms=10)
#> [1] 8.043785e-124
#> [1] -0.005592438 from rep="K2"

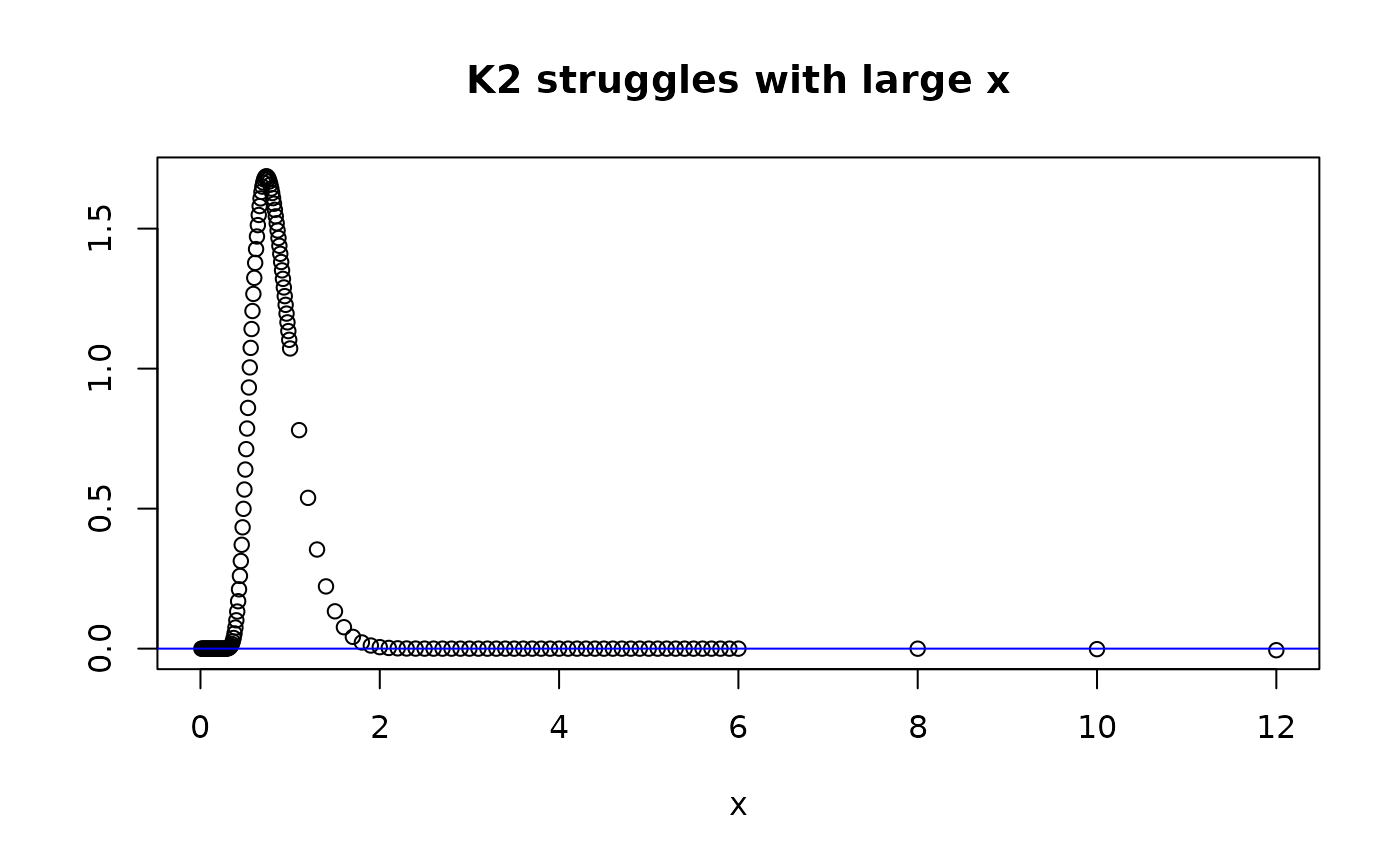
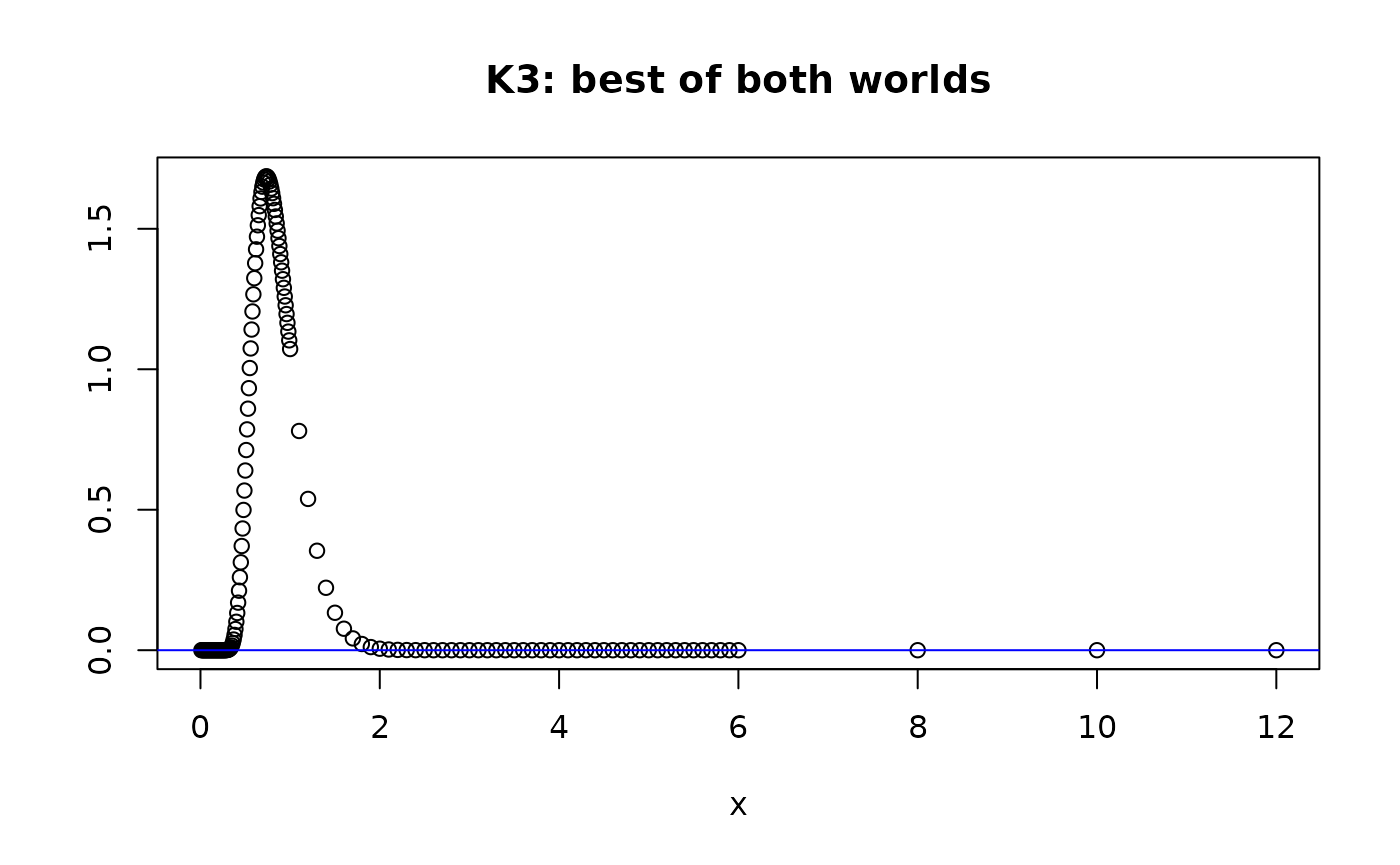
Since K1K1 is an alternating sum, if the number of terms is odd, we’ll see that K1K1 produces aberrant values that are positive, instead of negative. However K2K2 gets close to 0 for x=12x=12 but is still negative.

  • nterms=11
xdom <- c(seq(0.0,1,0.01), seq(1.1,6,.1), 8,10,12)
plot(xdom,dkolm(xdom,nterms=11,rep="K1"), main="K1 struggles with small x", ylab="", xlab="x")
abline(h=0,col="blue")
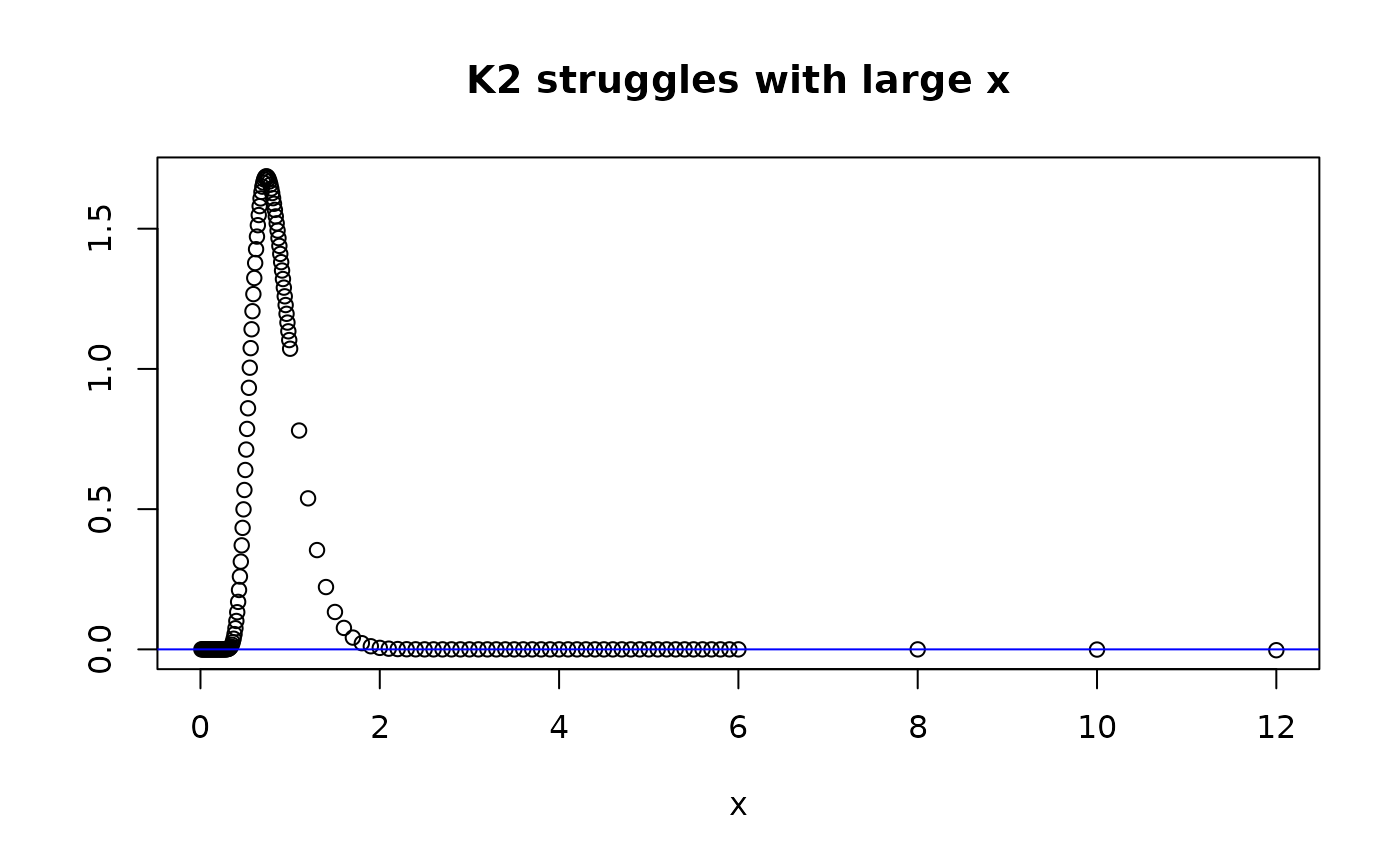
plot(xdom,dkolm(xdom,nterms=11,rep="K2"), main="K2 struggles with large x", ylab="", xlab="x")
abline(h=0,col="blue")

dkolm(12,rep="K2",nterms=11)
#> [1] -0.002983048
#> [1] -0.002983048 from rep="K2"

plot(xdom,dkolm(xdom,nterms=11,rep="K3"), main="K3: best of both worlds", ylab="", xlab="x")
abline(h=0,col="blue")

dkolm(12,rep="K3",nterms=11)
#> [1] 8.043785e-124
#> [1] -0.002983048 from rep="K2"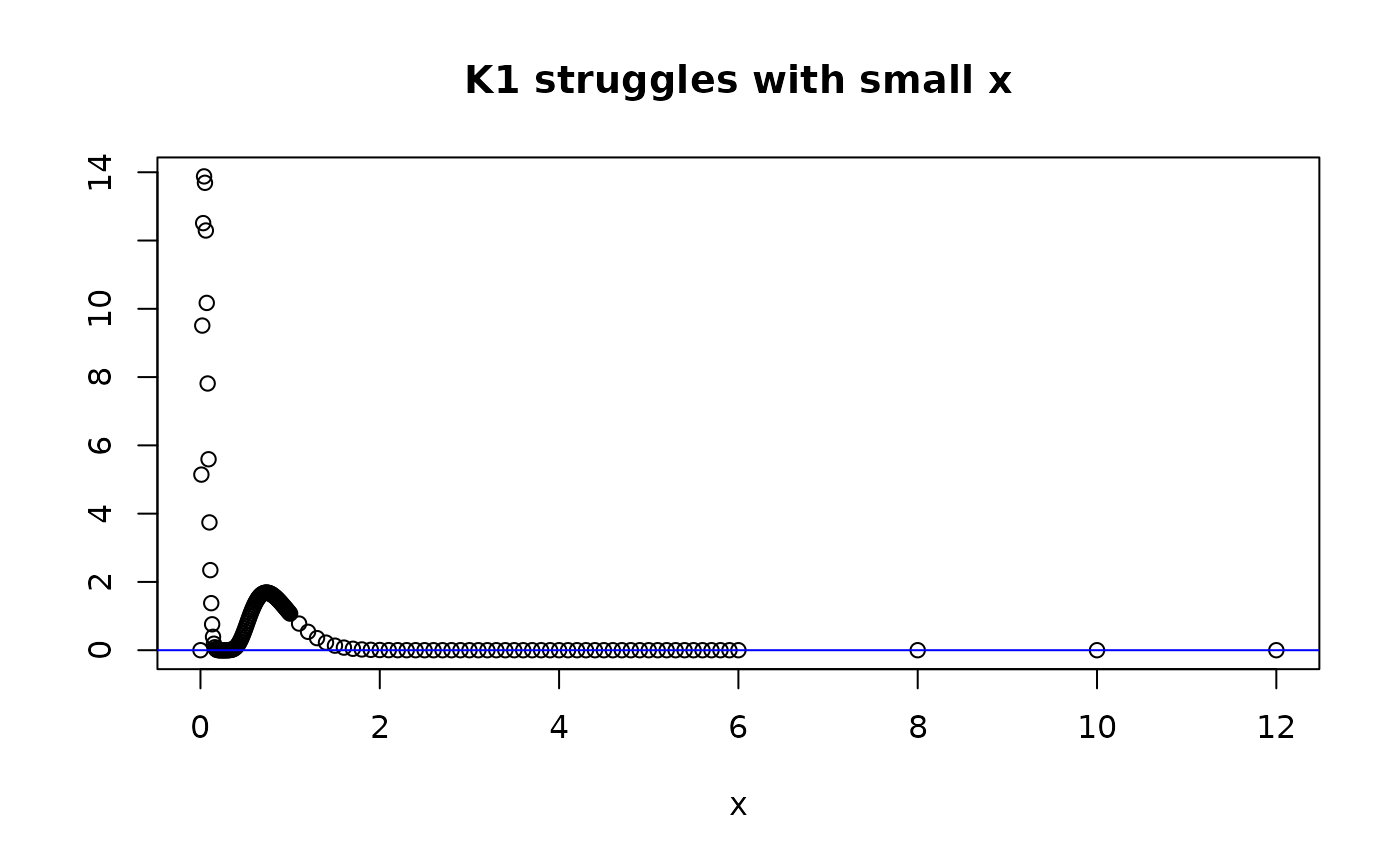

Random Variates

The most well-known formulation for random variates are from L(x/2) […], because this formulation is the scale mixture for a normal distribution to become a logistic distribution. Using that formulation we can easily derive how to get random variates for L(x), the Kolmgorov distribution. Turns out we just need to generate many i.i.d. exponential(rate=2) variables, sum them up with the squared integers in the denominators, and then take the square root of that sum.

#par(mfrow=c(2,2))
y_range_rv <- c(0,1.8)
x_range_rv <- c(0,4)
n <- 3e4; nterms <- 2000
##rv <- rkolm(1e4,500)

## this is from L(x/2)
rv <- 2*matrix(stats::rexp(n*nterms, rate=1), n, nterms) %*%
  matrix(1/c(1:nterms)^2,nrow=nterms)
range_rv <- range(rv)
x<-seq(range_rv[1],range_rv[2],0.01)
hist(sqrt(rv),freq=FALSE,breaks=130, 
     ylim=y_range_rv, xlim=x_range_rv, main="0.5*dkolm(x*0.5)", xlab="x")
lines(x,0.5*dkolm(x*0.5), col="red",lty=2, lwd=4)

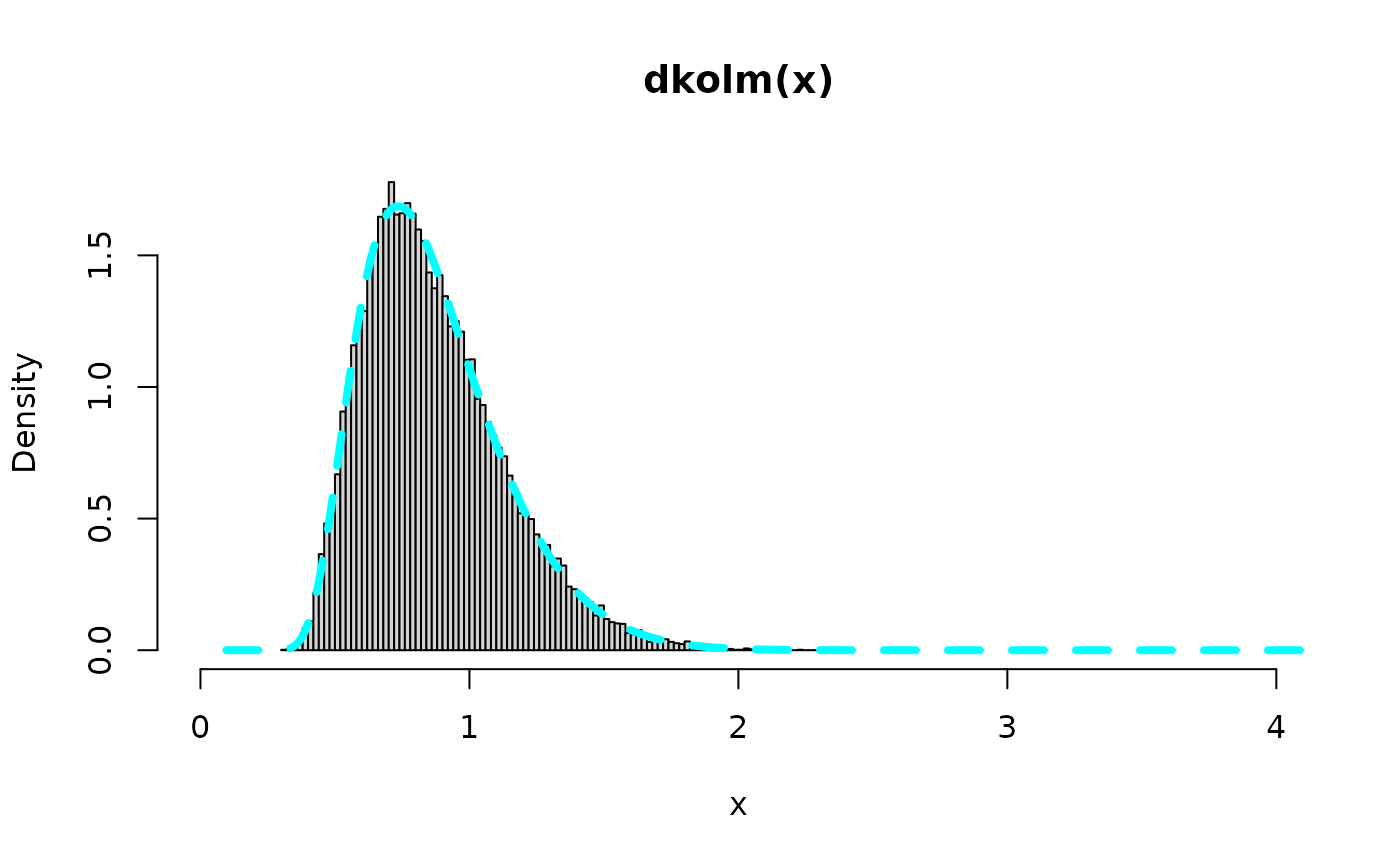
## this is from L(x)
rv <- 1*matrix(stats::rexp(n*nterms, rate=2), n, nterms) %*%
  matrix(1/c(1:nterms)^2,nrow=nterms)
range_rv <- range(rv)
x<-seq(range_rv[1],range_rv[2],0.01)
hist(sqrt(rv),freq=FALSE,breaks=130, 
     ylim=y_range_rv, xlim=x_range_rv, main="dkolm(x)", xlab="x")
lines(x, dkolm(x), col="cyan",lty=2,lwd=4)

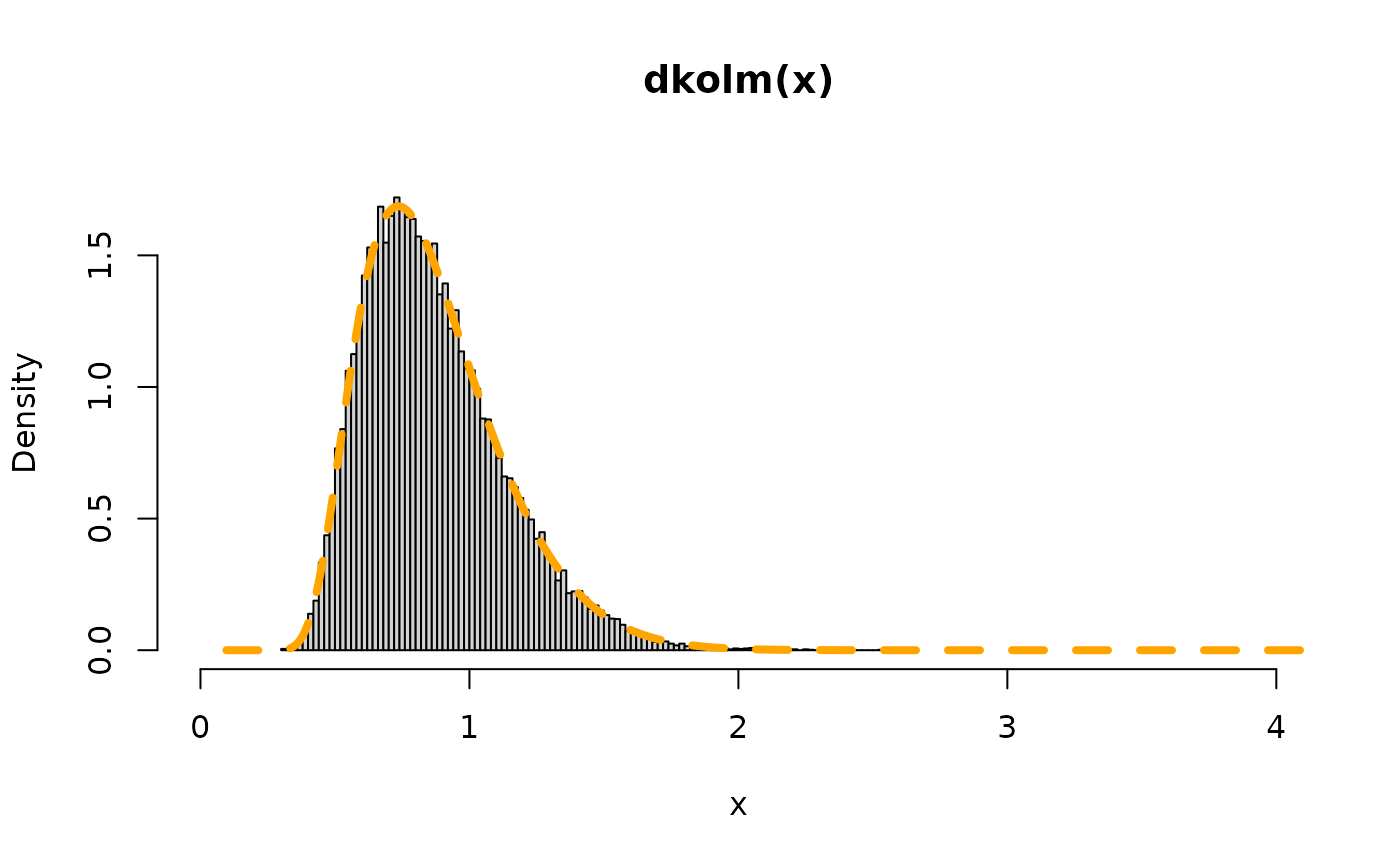
## equivalently, using rkolm()
## rkolm does all the steps, including the final sqrt()
hist(rkolm(n,nterms),freq=FALSE,breaks=130, 
     ylim=y_range_rv, xlim=x_range_rv, main="dkolm(x)", xlab="x")
lines(x, dkolm(x), col="orange",lty=2,lwd=4)


# rv <- rnorm(1e4, sd=2)
# range_rv <- range(rv)
# x<-seq(range_rv[1],range_rv[2],0.01)
# hist(rv,freq=FALSE,breaks=100)
# lines(x,0.5*dnorm(0.5*x), col="red",lty=2, lwd=4)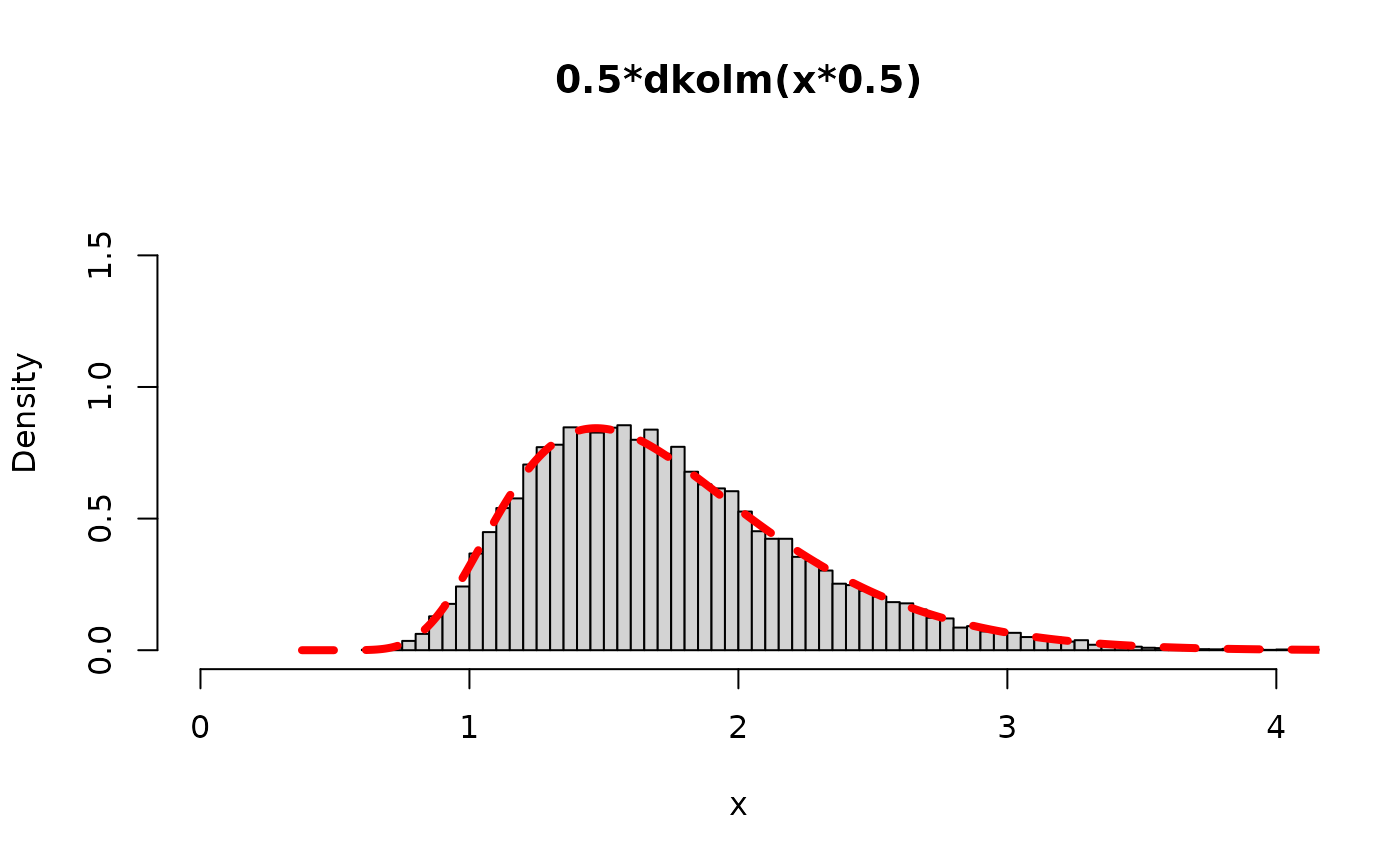

Check expected value – should be π2ln2=\sqrt{\frac{\pi}{2}}\ln2 = 0.8687312…. One could do this with their own code, or they can use mpvd:rkolm:

set.seed(102)

beg <- Sys.time()
rkdraw <- rkolm(5e4, nterms=5e2)
end <- Sys.time()
end-beg
#> Time difference of 0.8816485 secs

## Expected value
print(matrix(c(
  mean(rkdraw),
  sqrt(pi/2)*log(2)),
  ncol=1), 
  digits=20)
#>                        [,1]
#> [1,] 0.86871931109979994012
#> [2,] 0.86873116063615907212

## Variance
print(matrix(c(
  var(rkdraw),
  pi^2/12 - (sqrt(pi/2)*log(2))^2),
  ncol=1), 
  digits=20)
#>                         [,1]
#> [1,] 0.067522504088769474961
#> [2,] 0.067773203963865213950

## 2nd moment
print(matrix(c(
  mean(rkdraw^2),
  pi^2/12),
  ncol=1), 
  digits=20)
#>                        [,1]
#> [1,] 0.82219439511639869078
#> [2,] 0.82246703342411320303